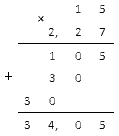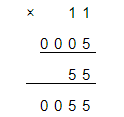Умножение десятичных дробей примеры для тренировки

Карточки с примерами на умножение десятичных дробей.
учебно-методический материал по математике (5 класс) на тему

Карточки с примерами на умножение десятичных дробей с ответами

Скачать:

Вложение	Размер
umnozhenie.doc	41.5 КБ

Предварительный просмотр:

9) 0,0005 · 100000;

10) 0,128 · 23,4375;

1) 1000000 · 6,0006;

1) 39,0625 · 0,0512;

12) 88,032 · 100000.

10) 100000 · 0,095;

11) 10000 · 1,0007;

1) 75,1456; 2) 62,027; 3) 0; 4) 0,0185; 5) 140,4302; 6) 241; 7) 6700,36; 8) 4167,1396; 9) 50; 10) 2; 11) 0,0483; 12) 0,0915.

1) 1,401; 2) 0,0001; 3) 1; 4) 38006; 5) 5; 6) 0,5487; 7) 40,27; 8) 20,7207; 9) 2288,8128; 10) 0; 11) 1,8008; 12) 0,03.

1) 58; 2) 23,8408; 3) 161,604; 4) 1; 5) 96,0126; 6) 16,522; 7) 2201,8; 8) 32,001; 9) 0,0777; 10) 3; 11) 0; 12) 0,7.

1) 6000600; 2) 67,0314; 3) 33,63; 4) 54,1198; 5) 0,0876; 6) 0; 7) 1; 8) 9,945; 9) 97; 10) 345,173; 11) 8,0016; 12) 0,0609.

1) 2; 2) 1352,338; 3) 20,2509; 4) 80; 5) 0,004; 6) 56,5552; 7) 0; 8) 0,2628; 9) 49; 10) 5,661; 11) 97,389; 12) 510,05.

1) 0; 2) 2592,84; 3) 9; 4) 0,0064; 5) 20005; 6) 6; 7) 4935,0423; 8) 18,0369; 9) 0,0301; 10) 6,066; 11) 41,0009; 12) 0,8.

1) 3971,728; 2) 0,0354; 3) 0; 4) 8408,2; 5) 82,0114; 6) 17; 7) 5,722; 8) 20,0124; 9) 14; 10) 10; 11) 0,33; 12) 3284,0619.

1) 0,374; 2) 121; 3) 3,375; 4) 2,6; 5) 0,1401; 6) 0,0094; 7) 6; 8) 0; 9) 2018,676; 10) 204,3774; 11) 282,796; 12) 8803200.

1) 0; 2) 0,0915; 3) 0,0693; 4) 1708,6624; 5) 35,121; 6) 290,848; 7) 6,3012; 8) 4020,3216; 9) 2; 10) 9500; 11) 700,05; 12) 241.

1) 841,9215; 2) 0,2988; 3) 0,071; 4) 1; 5) 0; 6) 2; 7) 3844,1576; 8) 52,444; 9) 0,0639; 10) 0,57; 11) 10007; 12) 0,0402.

По теме: методические разработки, презентации и конспекты

«История предков всегда любопытна для того, кто достоин иметь Отечество» — говорил Н.М.Карамзин. Изучать математику также интересно, если в этом помогает наша история.

Конспект урока с презентацией.

Конспект урока с презентацией.

Урок математики в 5 классе на тему «Умножение десятичных дробей»,урок открытия новых знаний,соответствует требованиям ФГОС.

Автор: Бурачкова Ирина СергеевнаОбразовательное учреждение: МБОУ «Клюквинская СОШИ» Верхнекетского районаНазвание кроссворда: Умножение десятичных дробей. Деление десятичных дробей на натуральное числ.

Особенности урока: урок — путешествие, прослеживается межпредметная связь с географией, экологией; практическая направленность заданий, показывает, где могут пригодиться знания математики; подоб.

Карточка по теме «Умножение десятичных дробей&quot.

Источник

Тренажер. Умножение десятичных дробей. 5 класс
тренажёр по математике (5 класс) на тему

Тренажер по теме «Умножение десятичных дробей» в 5 классе представлен в 12 вариантах. Тренажер можно использовать для отработки умножения десятичных дробей, для составления самостоятельной работы. Ко всем вариантам даны ответы.

Скачать:

Вложение	Размер
trenazher._umnozhenie_desyatichnyh_drobey.docx	17.65 КБ

Предварительный просмотр:

ТРЕНАЖЕР ПО ТЕМЕ «УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ». 5 КЛАСС.

10) 10000 · 0,00093;

12) 0,91407 · 0,007.

9) 0,00078 · 10000;

ОТВЕТЫ. Варианты №1 – 12.

По теме: методические разработки, презентации и конспекты

«История предков всегда любопытна для того, кто достоин иметь Отечество» — говорил Н.М.Карамзин. Изучать математику также интересно, если в этом помогает наша история.

Конспект урока с презентацией.

Конспект урока с презентацией.

Данная презентация предназначена для проведения устного счёта на уроках по теме «Умножение десятичных дробей», а также для обобщения материала по этой теме. Тренажёр может быть использован учите.

Интерактивная презентация-тренажёр к урокам математики по теме «Умножение десятичных дробей»Данная презентация предназначена для проведения устного счёта на уроках по теме «Умножение десятичных дробей.

Особенности урока: урок — путешествие, прослеживается межпредметная связь с географией, экологией; практическая направленность заданий, показывает, где могут пригодиться знания математики; подоб.

В данной презентации-тренажере представлены правило и задания для умножения десятичных дробей .Задания на слайдах оформлены как тест с выбором ответа. При нажатии на кнопку с номером, в слу.

Источник

5.5.4. Умножение десятичных дробей

I. Чтобы умножить десятичную дробь на натуральное число, нужно умножить ее на это число, не обращая внимания на запятую, и в полученном произведении отделить запятой столько цифр справа, сколько их было после запятой в данной дроби.

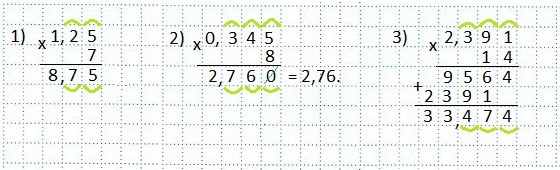
Примеры. Выполнить умножение: 1) 1,25·7; 2) 0,345·8; 3) 2,391·14.

Решение.

II. Чтобы умножить одну десятичную дробь на другую, нужно выполнить умножение , не обращая внимания на запятые, и в полученном результате отделить запятой справа столько цифр, сколько их было после запятых в обоих множителях вместе.

Примеры. Выполнить умножение: 1) 18, 2·0,09; 2) 3,2·0,065; 3) 0,54·12,3.

Решение.

III. Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр.

Примеры. Выполнить умножение: 1) 3,25·10; 2) 0,637·100; 3) 4,307·1000; 4) 2,04·1000; 5) 0,00031·10000.

Решение.

IV. Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.

Примеры. Выполнить умножение: 1) 28,3·0,1; 2) 324,7·0,01; 3) 6,85·0,01; 4) 6179,5·0,001; 5) 92,1·0,0001.

Источник

Повторение курса

1. Десятичная дробь – это форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.

Например, 1/100 = 0,01; 7/10 = 0,7 ; 19/1000 = 0,019

2. Запятая в десятичной дроби отделяет:

— целую часть от дробной;

— столько знаков, сколько нулей в знаменателе обыкновенной дроби.

3. Как перевести десятичную дробь в обыкновенную?

Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой в десятичной дроби.

4. Как обыкновенную дробь перевести в десятичную?

1 способ (хорошо работает, когда в знаменателе дроби: 2, 5, 20, 25… и т. д., то есть когда сразу понятно, на что надо умножать): домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось 10, 100, 1000 и т.д., а потом записать результат в десятичном виде.

2 способ: поделить числитель обыкновенной дроби на ее знаменатель (см. раздел сайта: 5 класс/десятичные дроби).

5. Сложение и вычитание десятичных дробей:

Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) натуральных чисел, в столбик: главное, чтобы запятая во втором числе стояла под запятой в первом. Например:

6. Умножение десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/умножение десятичных дробей):

Чтобы перемножить две десятичные дроби, нужно умножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом множителе и во втором множителе, а затем отделить полученное количество знаков в произведении, считая справа налево. Например:

7. Деление десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/деление десятичных дробей):

Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую в делителе вправо на столько позиций, пока он не станет целым. Потом на столько же позиций перенести запятую в делимом. Затем разделить получившиеся числа как обычно, в столбик. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом. Например:

1. Вычислите:

30,75 + 5,6136 21,6 — 13,823 7,05 * 0,0308 15,6672 : 3,84

5,52 + 994,48 406,01 — 75,997 507,8 * 3,005 0,03729 : 6,78

2. Найдите значение выражения:

а) (12 — 8,4) : 0,09 * 0,7 — 0,3 * (0,6 + 3,12) : (14,18 — 7,98) : 0,01

б) 10 * (0,056 : 0,8 * 700 — 40,2832) : (16 * 0,6 — 0 : 3,2) + 5,4 : 9 : 30

3. В летнем лагере за смену в 28 дней израсходовали 1 т картофеля. В первые 12 дней расход картофеля составил 38 кг в день. Каким будет расход картофеля в оставшиеся дни, если каждый день он будет одинаковым?

4. Найдите истинные высказывания. Расположите соответствующие им ответы в порядке возрастания, сопоставив их соответствующим буквам, и расшифруйте астрономический термин. Примеры, в которых допущена ошибка, решите правильно и запишите их в тетрадь.

Р 0,4 + 3 = 3,4 Д 9,1 — 1,05 = 8,05 А 0,8 * 0,04 = 0,032

У 6 + 0,12 = 0,18 Г 0,854 — 0,85 = 0,04 К 5 : 1000 = 0,05

Н 0,25 + 0,5 = 0,3 Б 0,5 * 3 = 0,15 Т 3,6 : 9 = 0,4

О 3,28 + 1,3 = 4,58 И 4 * 1,7 = 6,8 Я 12,3 : 5 = 24,6

Е 2,6 — 0,01 = 2,59 Ж 17,2 * 10 = 1,72 С 0,056 : 0,7 = 0,08

5. У дачника было три улья. С первого улья он получил 24,8 кг мёда, со второго — на 6,4 кг меньше, чем с первого, а с третьего — половину того, что собрал с первых двух ульев вместе. Весь мёд он разложил поровну в 18 банок. По скольку килограммов мёда было в каждой банке?

6. Существует версия, что «золотое руно», за которым отправились аргонавты в Колхиду, есть не что иное, как секрет выделки одного растения. Его-то и продавали на вес золота в Древнем мире. Голубой венчик этого растения — это «цвет неба», — считали жрецы Исиды и носили одежды только из этого растения. Что это за растение? Чтобы ответить на этот вопрос, вычислите рационально:

18,7 * 3,6 — 3,6 * 8,7 + 4,4

17,3 * 18,9 — 18,9 * 3,1 + 15,8 * 18,9

37,2 * 18,2 — 18,2 * 21,3 + 19,2 * 15,9 + 15,9 * 2,6

Е=40,4 ; Д=36 ; С=8 ; Н=567 ; У=684,18 ; Л=636 ; Б=728 ; И=872.

7. Соком этого растения был отравлен король датский, отец Гамлета. Сейчас оно входит в состав мазей для лечения простуды, бронхита, плеврита, т. к. вещества, входящие в его состав, оказывают спазмолитическое действие. Что это за растение? (Результат каждого действия даёт букву.)

227,36 : (865,6 — 20,8 * 40,5) * 8,38 + 1,12 — 44

А=842,4 ; К=844,2 ; Е=23,2; С=93,5 ; Е=9,8 ; О=84,24 ; Н=82,124 ; Б=83,244 ; Л=39,244 ; Я=83,2.

8. Этого симпатичного зверька на латыни именовали «королём зелени». Назовите его:

(68,344 — 3,09 : 1,5) : 7,3 + 2,7 * 8,5 — 2,03

Б=26 ; О=2,06 ; В=2,6 ; И=66,284 ; А=681,38 ; Л=9,08 ; А=9,8 ; Ц=98 ; Н=229,5 ; Е=0,3203 ; Р=22,95 ; К=32,03 ; К=30.

9. Выполните действия и округлите полученный результат с точностью:

• до десятков: 2987,4 + 7,85; 100,1 — 47,907; 39,5 * 5,09; 163,846 : 0,79
• до единиц: 82,435 + 7,0684; 203 — 75,48; 470,5 * 0,804; 0,43236 : 0,045;
• до десятых: 205,038 + 9,47; 4,2 — 1,517; 320 * 0,0564; 0,06111 : 0,063;
• до сотых: 1,514 + 0,4872; 5,1002 — 0,005; 5,7 * 0,053; 0,649636 : 0,806

Источник

Умножение десятичных дробей

О чем эта статья:

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6
• 21,10200000 = 21,102

Основные свойства
Дробь не имеет значения, при условии, если делитель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Пример 2. Перевести 37/1000 в десятичную дробь.

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Принципы умножения десятичных дробей

С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби.

Свойства умножения десятичных дробей

Переместительное свойство умножения — от перестановки мест множителей произведение не изменяется. ab = ba Сочетательное свойство умножения — чтобы умножить число на произведение двух чисел, нужно сначала умножить его на первый множитель, затем полученное произведение умножить на второй множитель. (ab)c = a(bc) Распределительное свойство умножения относительно сложения — чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить. a(b + c) = ab + ac Распределительное свойство умножения относительно вычитания — чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе. a(b — c) = ab — ac

Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.

Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:

«−−»	минус на минус дает плюс
«−+»	минус на плюс дает минус
«+−»	плюс на минус дает минус
«++»	плюс на плюс дает плюс

Числа с единицей и нулями (10, 100, 1000 и т. д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:

• Чтобы умножить число на разрядную единицу, достаточно к числу справа дописать столько нулей, сколько их содержит разрядная единица.
• Чтобы разделить число на разрядную единицу, достаточно от числа справа отбросить столько нулей, сколько их содержит разрядная единица.

Как умножать десятичные дроби в столбик

Чтобы перемножить десятичные дроби нужно сделать три шага:

1. Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.
2. Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.
3. Полученную цифру отсчитать справа налево и поставить запятую.

Пример 1. Перевести 5,4 в смешанное число.

Как решаем:

Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых:

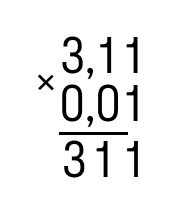
Получаем: 311 ∗ 001 = 311.

Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую).

Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы

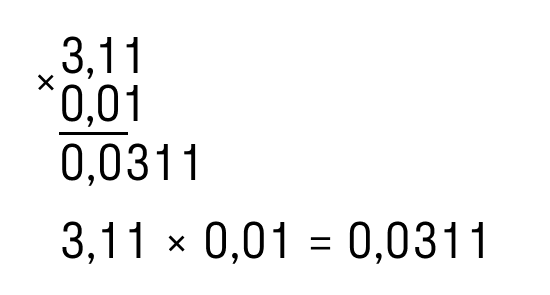
Ответ: 3,11 ∗ 0,01 = 0,0311.

Примеры умножения десятичных дробей столбиком:

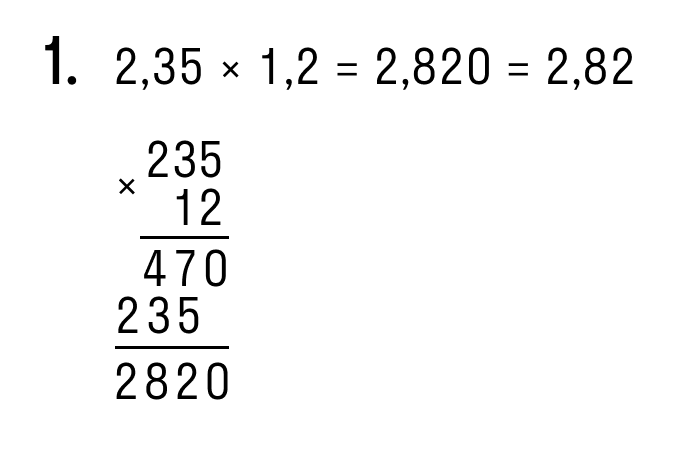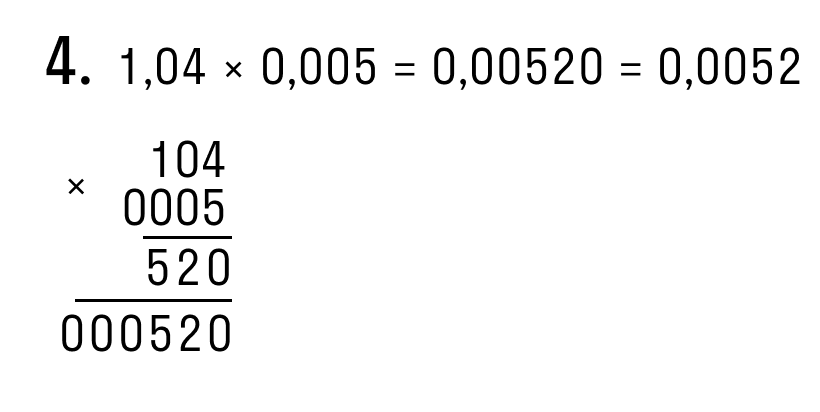Как умножать десятичные дроби на натуральные числа

Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями. Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!

Пример 1. Умножить десятичную дробь 2,27 на целое число 15.

умножить столбиком данные числа и отделить два знака запятой.

Ответ: 15 ∗ 2,27 = 34,05.

Пример 2. Умножить 11 на 0,005.

умножить столбиком данные числа и отделить три знака запятой.

Ответ: 11 ∗ 0,005 = 0,055.

Пример 3. Умножить 0,1557.. на 3.

1. Округлить бесконечную дробь: 0,1557..≈ 0,156
2. Полученное число умножить на 3: 0,156 ∗ 3 ≈ 0468.

Ответ: 0,1557.. ∗ 3 ≈ 0468..

Как умножать десятичные дроби на 10, 100, 1000

Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.

• 1,15 ∗ 10 = 11,5;
• 22,345 ∗ 100 = 2 234,5;
• 8,99 ∗ 1 000 = 8 990;
• 0,54678 ∗ 10 000 = 5467,8;
• 0,07 ∗ 1 000 = 70;
• 0,00033 ∗ 100 = 0,033.

Как умножать десятичные дроби на 0,1, 0,01, 0,001

Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.

• 34,9 ∗ 0,1 = 3,49;
• 1,8 ∗ 0,1 = 0,18;
• 145,7 ∗ 0,01 = 1,457;
• 9655,1 ∗ 0,001 = 9,6551;
• 11,9 ∗ 0,0001 = 0,00119.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 3/5 на 0,9.

Записать 0,9 в виде обыкновенной дроби:

Ответ: 3/5 ∗ 0,9 = 0,54.

Пример 2. Умножить 0,18 на 3 1/4.

Записать 3 1/4 в виде десятичной дроби:

Произвести умножение в столбик или при помощи калькулятора:

Ответ: 0,18 ∗ 3 1/4 = 0,585.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Увлекательные задачи по математике для детей 7–13 лет

Источник