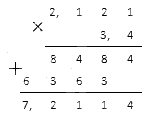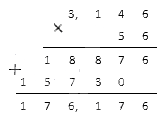Рациональные числа примеры для тренировки

Некоторые упражнения на действия с рациональными числами
учебно-методический материал по алгебре на тему

Скачать:

Вложение	Размер
nekotorye_uprazhneniya_na_deystviya_s_ratsionalnymi_chislami.doc	23 КБ
o_professii_uchitelya.doc	30.5 КБ
formirovanie_vychislitelnykh_navykov.doc	23.5 КБ

Предварительный просмотр:

НЕКОТОРЫЕ УПРАЖНЕНИЯ НА ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ

В преподавании математики в 6-х классах часто сталкиваешься с фактом, что учащиеся часто формально усваивают действия с рациональными числами, так называемые правила знаков заучиваются без должного понимания. Одна из причин формального усвоения этих правил заключается в том, что в наших задачниках, в текстах различных самостоятельных работ даются по преимуществу прямые примеры:

Находятся ученики, которые, выполнив вычисление в примере (-5) + (-9) получают +14, аргументируя свой ответ словами: «минус на минус дает плюс».

В своей практике я предлагаю учащимся примеры такого рода, в которых самим учащимся приходится определять знаки компонентов действий, причем в ряде случаев ответы допускают несколько вариантов. Отсутствующие знаки заменены многоточиями. Вот некоторые из этих примеров:

Такие примеры могут даваться как в порядке устных упражнений (причем учитель должен требовать от ученика объяснения своих ответов) так и могут включаться в контрольную работу.

В дальнейшем учитель может заменять конкретные числа буквенными данными и предлагать указывать знаки чисел a, b и c:

Предварительный просмотр:

О ПРОФЕССИИ УЧИТЕЛЯ

Как разнообразен мир – каких только профессий нет в нём на сегодняшний день! На этом многообразном фоне профессия учителя не всегда привлекает внимание, но заслуживает его Мы, учителя заняты воспитанием нашего будущего, мы воспитываем тех, кто завтра сменит нынешнее поколение. Брак в нашей работе – катастрофа, ведь испортив «живой материал», получишь испорченную человеческую единицу, которой приходится жить дальше в обществе.

Легко ли стать учителем? Судите сами: эта профессия требует не только всесторонних знаний, но и безграничной душевной щедрости, бескорыстной любви к детям, ко ВСЕМ детям, а не только к «паинькам» и «умницам». Мало – приходить на работу, провести уроки и уходить домой с лёгкой душой. Отдавать всего себя ежедневно, «гореть» на работе – вот гарантия того, что дети полюбят науку, полюбят труд, обретут незыблемые нравственные принципы.

Такой труд нелёгок, он требует постоянного источника вдохновения и творчества. Учитель черпает его из сознания своего долга перед настоящим и будущим. Его творчество питают животворные идеи великих учителей: К.Д. Ушинского, Н.К.Крупской, А.В.Луначарского, А.С.Макаренко, В.А.Сухомлинского и многих других.

В учебно-воспитательном процессе одним из самых главных и сложных моментов является пропорциональность обучения и воспитания, т.е. их соотношение. По этому поводу хорошо сказал Сухомлинский:

«Уже в первые годы педагогической работы мне стало ясно, что подлинная школа — это не только место, где дети приобретают знания и умения. Учение — очень важная, но не единственная сфера духовной жизни ребенка. Чем ближе я присматривался к тому, что мы все привыкли называть учебно-воспитательным процессом, тем больше убеждался, что подлинная школа — это многогранная духовная жизнь детского коллектива, в котором воспитатель и воспитанник объединены множеством интересов и увлечений. Человек, который встречается с учениками только на уроке, — по одну сторону учительского стола, а по другую учащиеся, — не знает детской души, а кто не знает ребенка, тот не может быть воспитателем. Для такого человека за семью печатями закрыты мысли, чувства и стремления детей.»

И далее: «С болью видишь, как даже у знающих свой предмет учителей

воспитание иногда превращается в ожесточенную войну только потому, что никакие духовные нити не связывают педагога и учеников, и душа ребенка — застегнутая на все пуговицы рубашка. Главная причина уродливых, недопустимых отношений между наставником и питомцем, имеющих место в отдельных школах, — это взаимное недоверие и подозрительность: иногда учитель не чувствует сокровенных движений детской души, не переживает детских радостей и горестей, не стремится мысленно поставить себя на место ребенка. Выдающийся польский педагог Януш Корчак в одном из писем напоминает о необходимости возвыситься к духовному миру ребенка, а не снисходить к нему. Это очень тонкая мысль, в сущность которой нам, педагогам, надо глубоко вникнуть».

Эти слова великого отечественного педагога считаю своим личным кредо и руководствуюсь ими в своей работе.

Предварительный просмотр:

ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ

Формирование у учащихся прочных вычислительных навыков является одной из главнейших задач их подготовки к практической деятельности в жизни. В деле повышения вычислительной культуры учащихся большую роль играют числовые подстановки, проверка с их помощью правильности выполнения тождественных преобразований, решения уравнений и т. д. Такую проверку желательно начинать уже при знакомстве с понятиями «коэффициент» и «показатель степени» и практиковать в дальнейшем при изучении курса алгебры 7 класса.

Иногда чтобы показать роль алгебры в упрощении вычислений полезно предлагать числовые подстановки с двойным заданием: вычислить значение данного выражения при известных значениях букв, входящих в него, и вычислить значение выражения, предварительно упростив его. Особенно полезны подобные действия при раскрытии скобок и при умножении многочленов с приведением подобных членов. При этом желательно подбирать такие значения букв, при которых значение выражения вычисляется устно.

Применение алгебры к вычислениям можно продемонстрировать следующими примерами:

(20,1) 3 ; (49,9) 3 ; (4 4/5) 3 ; (10 ¼) 3 . При решении таких примеров целесообразно пользоваться формулами (а ± b) 3 .

Большинству учащихся не всегда легко даются вычисления с десятичными дробями, поэтому нужно уделять больше внимания десятичным дробям, при этом не ослабляя внимания к дробям обыкновенным и особенно к смешанным числам.

Полезно проводить арифметическую подготовку к рассмотрению различных вопросов алгебры. Например, перед изучением алгебраических выражений можно провести занятие, посвященное чтению и записи алгебраических выражений:

1. Прочитайте 4,1 + 9½ ∙ ¾ — (0,7) 3 ;

2. Запишите и вычислите:

а) удвоенную разность чисел 1,3 и 0,95;

б) произведение суммы чисел 1 ¾ и 5 ¼ на разность чисел 0,784 и 0,684;

в) произведение частного от деления числа 166 на 83 и суммы чисел135 и 49.

Такие упражнения можно провести в виде математического диктанта.

По теме: методические разработки, презентации и конспекты

Не все дети любят считать. Но забавная «Пчелка» поможет проявить интерес даже к такой трудной теме. Эта презентация наверняка понравится вашим ученикам. А может использоваться и родителями.

Разработка урока с презентацией сказочное путешествие по теме: «Действия с рациональными числами» в 6 классе по учебнику Н.Я. Виленкина.

Обобщающий урок по теме «Все действия с рациональными числами» для 6 класса выполнен с применением игровых технологий. Сюжет урока — путешествие под водой с целью поиска пиратского клада. В данной мет.

Обобщить знания учащихся по темам « Сложение, вычитание, умножение рациональных чисел»; совершенствовать вычислительные навыки; развивать активность, самостоятельность, познавательный интерес, л.

В данной статье представлено описание урока обобщения и систематизации знаний по теме «Действия с рациональными числами и свойства действий с рациональными числами». Урок посвящен повторению правил, о.

Примеры на усвоение основных действий с рациональными числами.

Контрольная работа по теме «Модуль числа. Действия с рациональными числами» (6 класс).

Источник

Тренажер действия с рациональными числами
тренажёр по математике (6 класс)

Тренажер действия с рациональными числами 6 класс

Скачать:

Вложение	Размер
trenazher_deystviya_s_ratsonalnymi_chislami.docx	18.42 КБ

Предварительный просмотр:

Таблица № 1. Действия с рациональными числами.

По теме: методические разработки, презентации и конспекты

Не все дети любят считать. Но забавная «Пчелка» поможет проявить интерес даже к такой трудной теме. Эта презентация наверняка понравится вашим ученикам. А может использоваться и родителями.

Разработка урока с презентацией сказочное путешествие по теме: «Действия с рациональными числами» в 6 классе по учебнику Н.Я. Виленкина.

Обобщающий урок по теме «Все действия с рациональными числами» для 6 класса выполнен с применением игровых технологий. Сюжет урока — путешествие под водой с целью поиска пиратского клада. В данной мет.

Обобщить знания учащихся по темам « Сложение, вычитание, умножение рациональных чисел»; совершенствовать вычислительные навыки; развивать активность, самостоятельность, познавательный интерес, л.

Урок,объяснение нового материала на базе знаний 5 класса в виде устной работы,которая позволяет самим учащимся рассказать о свойствах действий с рациональными числами.На уроке ребята отрабатывают пере.

В данной статье представлено описание урока обобщения и систематизации знаний по теме «Действия с рациональными числами и свойства действий с рациональными числами». Урок посвящен повторению правил, о.

Контрольная работа по теме «Модуль числа. Действия с рациональными числами» (6 класс).

Источник

Тренажер сложение и вычитание рациональных чисел
методическая разработка по математике (6 класс)

тренажер сложение и вычитание рациональных чисел

Скачать:

Вложение	Размер
trenazher_dlya_6_klassa_po_teme_slozhenie_i_vychitanie_polozhitelnyh_i_otritsatelnyh_chisel.docx	36.45 КБ

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Можно использовать для проверки знаний по теме.

Материал, содержащийся в данном тесте, позволяет помочь учащимся научиться уверенно решать как стандартные, так и нестандартные задачи.Тест предназначен как для учащихся, проявляющих интерес к и.

Я работаю учителем математики 18-ый год, более 10 лет из которых были посвящены открытию для себя, затем изучению и попыткам (иногда успешным, иногда нет) технологизировать процесс обучения, осн.

Урок обобщения и систематизации знаний для учащихся 6 класса. Используются различные виды работы в учащимися.

ПРОЕКТРеализация требований ФГООС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел» Выполнил слушатель учебного курса«Актуальные проблемы развития профессион.

Презентация кПРОЕКТРеализация требований ФГООС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел».

Контрольная работа по математике 6 класс. Мерзляк.

Источник

Действия с рациональными числами: правила, примеры, решения

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .

Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .

Сложение противоположных рациональных чисел

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).

К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .

Осуществим сложение дробей с разными знаменателями:

6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45

Ответ: 0 , 6 + 5 9 = 1 7 45 .

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.

Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .

Сложение отрицательных рациональных чисел

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .

Решение

Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:

​​​​​​

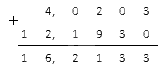
Полученному результату присваиваем знак минус: — 16 , 2133 .

Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55

Ответ: 4 , ( 36 ) — 1 5 = 4 9 55

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .

Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7

Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7

Ответ: 2 7 + — 5 3 7 = — 5 1 7

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Произведение любого рационального числа a на нуль есть нуль.

Используя переместительное свойство умножения, получим: 0 · а = 0 .

К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .

Умножение на единицу

Умножение любого рационального числа a на 1 дает число a .

Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .

Умножение взаимообратных чисел

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .

К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .

Решение

Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .

Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .

Ответ: 0 , 5 · 6 25 = 3 25

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .

Решение

Перемножим десятичные дроби столбиком:

Ответ: 2 , 121 · 3 , 4 = 7 , 2114

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Необходимо найти произведение чисел: — 3 3 8 и 2 1 2

Решение

Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2

Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16

Ответ: — 3 3 8 · 2 1 2 = — 8 7 16

Умножение отрицательных рациональных чисел

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .

Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .

Перемножим их столбиком:

Полученный результат и будет являться искомым произведением.

Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Необходимо выполнить действие деления 3 1 3 : — 1 1 6

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .

Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7

Ответ: 3 1 3 : — 1 1 6 = — 2 6 7

Источник