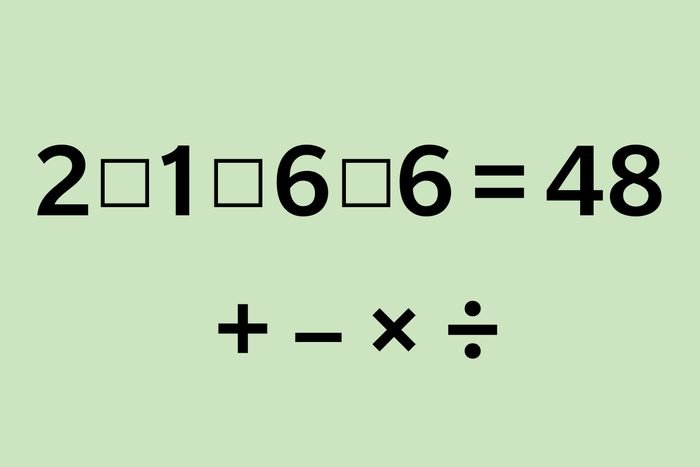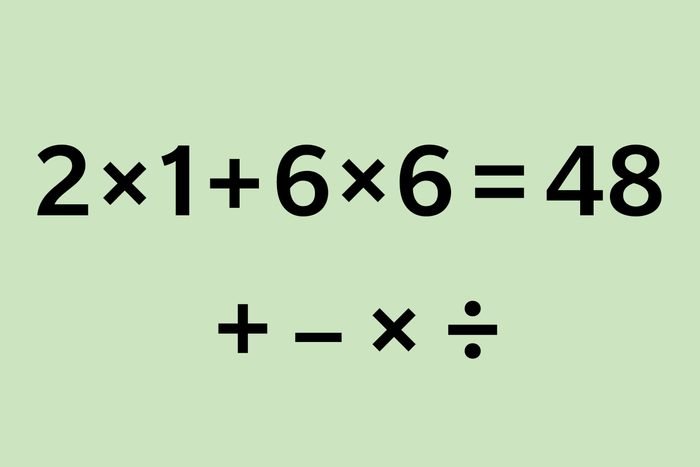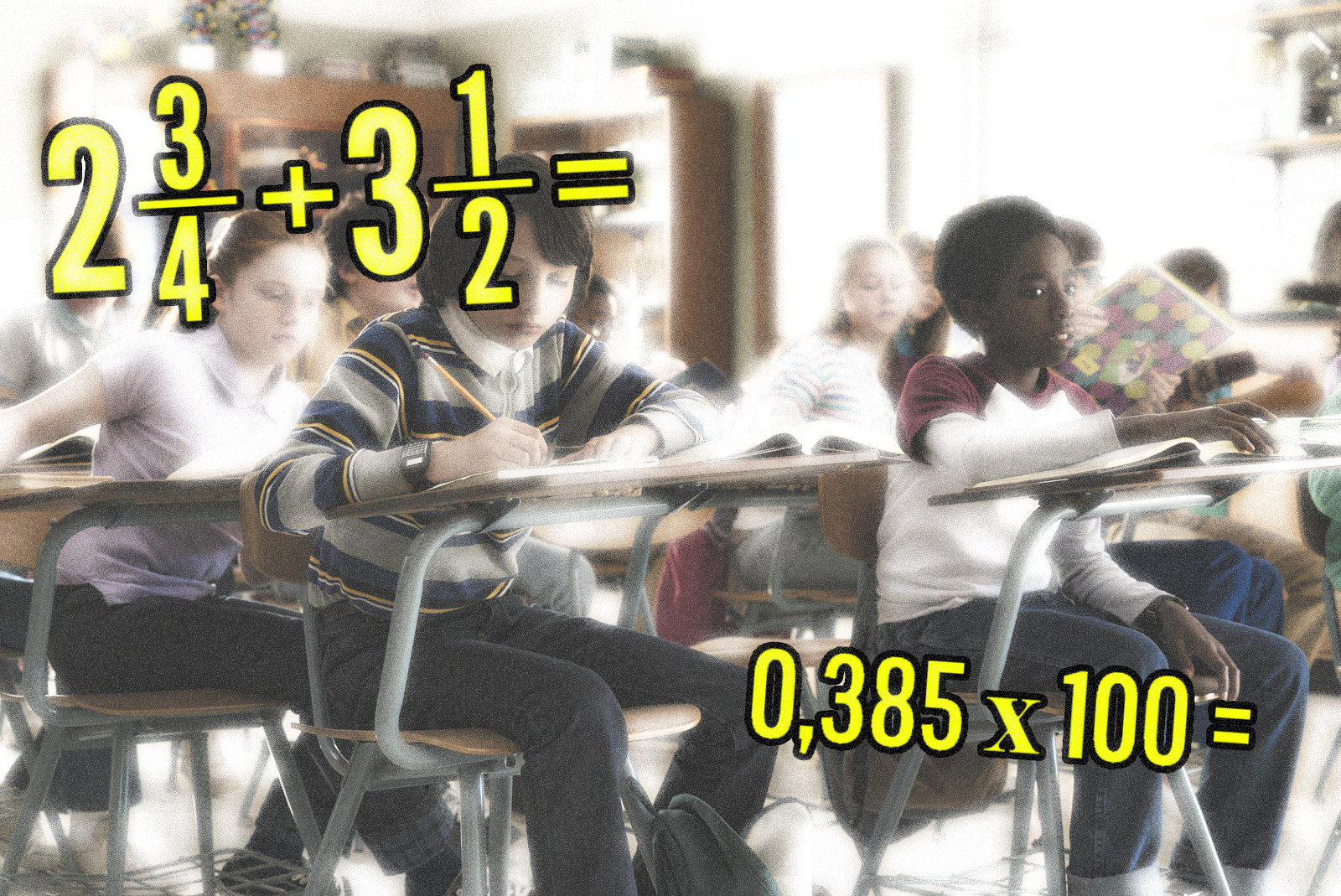Математика разминка для ума

Игры для мозга: 30 математических головоломок для проверки вашего ума (с ответами)

Математические задачи для детей и взрослых, которые помогут отлично размять мозг и натренировать память

Кто сказал, что математика не может быть веселой?! Эти математические головоломки с ответами – восхитительный вызов вашим способностям.

Понятно, что математика не всем нравится. Много часов над сложными уравнениями могут заставить скучать кого угодно. Но когда математические задачи выходят за рамки школьной обстановки, на решение нет временных ограничений и есть забавная концепция, более причудливая, чем просто найти Х, они могут стать увлекательным занятием для детей (и взрослых, конечно!). Головоломки проверяют наш мозг и навыки критического мышления, обеспечивают конструктивное, образовательное времяпрепровождение и представляют наглядные примеры уроков математики, которые мы действительно сможем использовать в реальной жизни.

Математические головоломки бывают самых разных видов. Некоторые, более простые, требуют элементарных вычислений, чтобы найти верное решение. Другие больше похожи на логические ребусы, заставляющие искать закономерность. Третьи представляют задание посредством картинок, отлично подходя для наглядного обучения.

Забавные математические задачки подобранные редакцией 1GAI.ru содержат всего понемногу! Если любите искать решения, предлагаем вам увлекательные математические головоломки – взрослые и детские. А если предпочитаете избежать сложной математики, есть отличные загадки для детей.

Математические задачки для детей

1. Суммы символов

Сможете ли вы сделать это уравнение правильным, используя три из следующих четырех символов: +, −, x и ÷ ?

Порядок операций не применяется, дроби и отрицательные числа не используются.

Ответ:

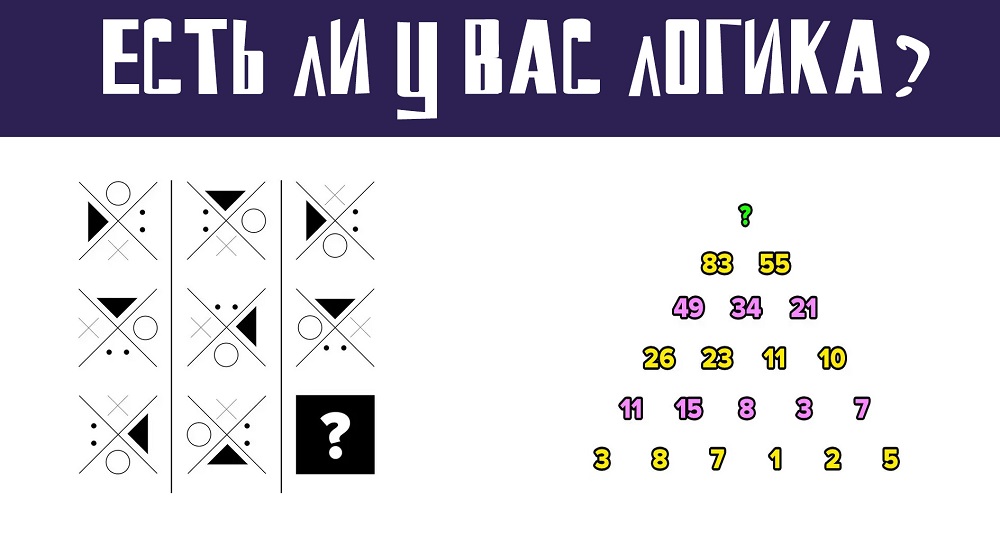
2. Числовой куб

Какое число должно заменить вопросительный знак?

Ответ: 9.

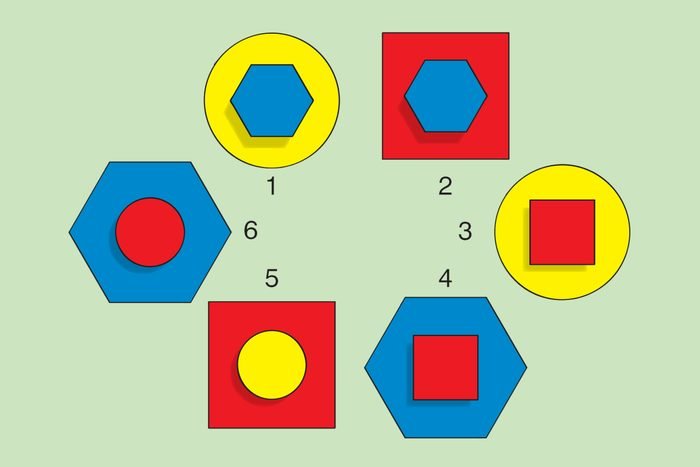
3. Разноцветная неразбериха

Какая цифра (1-6) окрашена неправильно?

Ответ: 6 – эта цифра должна быть желтой.

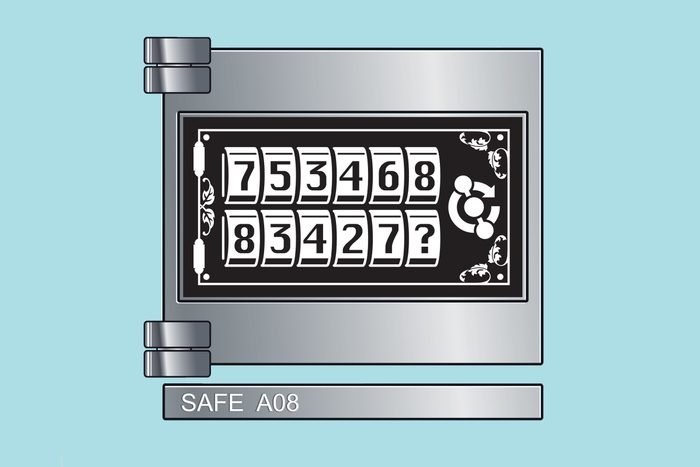
4. Код сейфа No1

Чтобы открыть сейф, надо заменить вопросительные знаки правильными цифрами. Вы можете найти подсказку, определив закономерность показанных чисел.

Ответ: 1 и 4. Они расположены в группах из двузначных чисел, оканчивающихся на 7 и возрастающих в обеих строках.

5. Код сейфа No2

Чтобы вскрыть этот сейф, вы должны заменить знаки вопроса правильными цифрами. Опять же, ищите закономерность в показанных числах.

Ответ: 1 и 2. Каждое число в нижнем ряду – это число над ним минус 3.

6. Яблочко

Сколько очков набирает лучник B, зная, что общий балл лучника A равен 55 и что разные очки зарабатываются в десяти зонах по возрастанию к центру?

Ответ: 30. Внешняя зона приносит 1 очко, затем 2, 3 и т.д. Центральная зона приносит 10 очков. 5 + 8 + 8 + 9 = 30.

7. Страйк

Какие кегли нужно сбить, чтобы набрать ровно 100 очков? (Подсказка: их три!)

Ответ: 13, 39 и 48.

Числовые головоломки

8. Фейерверк

Каждый фейерверк (AF) содержит 6 звезд. Определите, какой фейерверк не был запущен, зная, что в каждом из них 1, 2 или 3 звезды соответствующего цвета?

Ответ: C. Всего в фейерверке 9 желтых звезд, но в воздухе только 6. Посчитайте (9 — 6 = 3), и вы обнаружите, что 3 желтые звезды еще не были запущены.

9. Цифровая панель

Найдите, какое число должно заменить вопросительный знак, чтобы сформировать точные уравнения, зная, что в каждой строке показаны три числа (т.е. два образуют числовое выражение)?

Ответ: 6. Прочтите каждую строку следующим образом:

10. Большая игра

Какие цифры следует заменить вопросительными знаками?

Ответ: 563412. Все остальные номера билетов представляют собой комбинации чисел 12, 34 и 56, а 563412 – их последняя возможная комбинация.

11. На время

Спортсмен-победитель пробежал дистанцию за 15 секунд, следующий за ним – за 21 секунду и т.д. Сколько секунд потребуется шестому спортсмену, чтобы пересечь финишную черту?

Ответ: 39 секунд. Формула: 15 + (1 + 5) = 21; 21 + (2 + 1) = 24; 24 + (2 + 4) = 30; 30 + (3 + 0) = 33; 33 + (3 + 3) = 39.

12. Кредитный рейтинг

Какая цифра отсутствует на нижней кредитной карте?

Ответ: 8. Число, образованное двумя первыми цифрами, всегда удваивается. 12, 24, 48, 96, 192 на верхней карте и 23, 46, 92, 184, 368 на нижней.

13. Отсутствующий сценарий

Определите, какое число должно заменить вопросительный знак, зная, что всегда отображаются двузначные числа?

Ответ: 6. Читайте слева направо, воспринимая запись как ряд чисел, которые всегда делятся на четыре (или на два, если чередовать верхнюю и нижнюю строки). 96 ÷ 4 = 24; 24 ÷ 4 = 6 (или 06); 48 ÷ 4 = 12.

14. Школьная доска

Какое число должно заменить вопросительный знак?

Ответ: 3. Цифры под линией – это среднее значение трех чисел в столбце выше.

Головоломки с математикой и логикой

15. Безопасный код

Чтобы сейф открылся, вы должны заменить вопросительный знак правильной цифрой. Ее можно найти, применив логический подход к показанным числам. Методы могут включать в себя вычисление, инверсию, повторение, хронологическую последовательность или формирование восходящих и нисходящих рядов.

Ответ: 6. Сгруппировав ряд двузначных чисел, вы добавляете восемь к верхнему двузначному числу (75, 34, 68), чтобы получить нижнее (83, 42, 76).

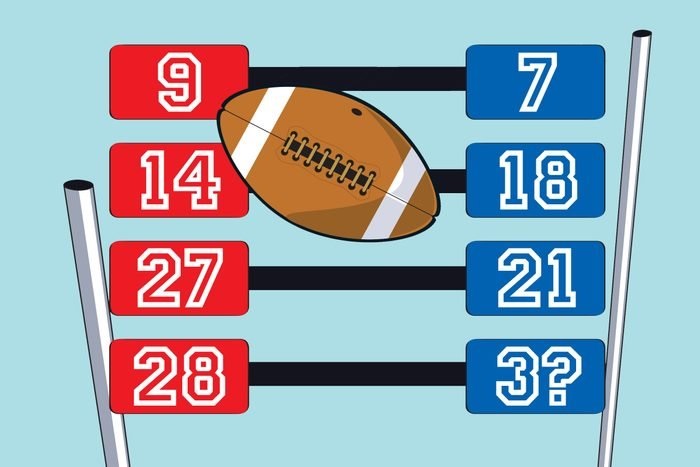
16. Подсчет очков

Какая цифра должна заменить вопросительный знак?

Ответ: 6. Разница в баллах образует следующий ряд: –2, +4, –6, +8. Чередование в колонке обнаруживает следующие две серии: 7, 14, 21, 28; 7, 14, 21, 28; 9, 18, 27, 36.

17. Солнечная сила

Сколько энергии будет генерировать новейшая солнечная панель?

Ответ: 04,96 В. Число перед десятичной точкой такое же, как количество столбцов на панели, а число после определяется количеством ячеек.

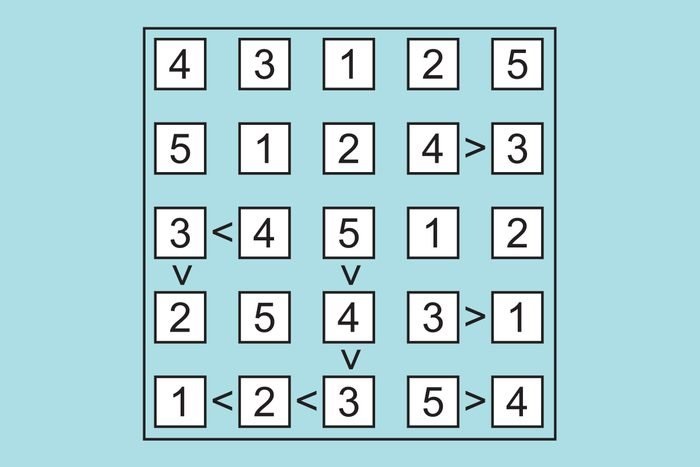
18. Футошики – японская игра

Заполните сетку 5 x 5 числами от 1 до 5, используя их однократно в строке и столбце и следуя указанным символам больше/меньше. Есть только одно верное решение, достигаемое исключительно с помощью логики и ясного мышления!

Ответ:

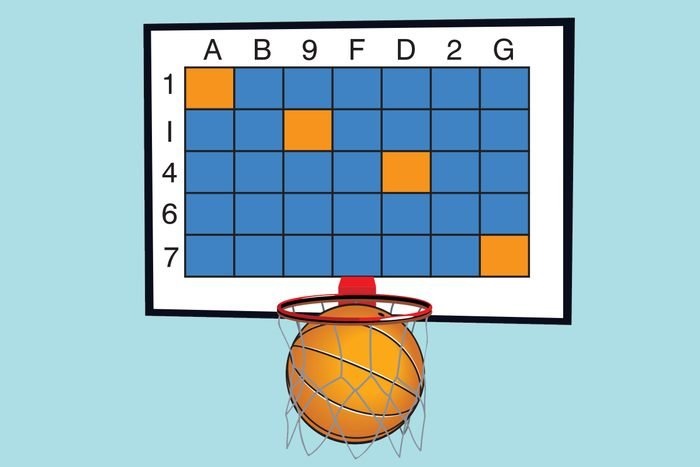
19. Мишень

Очко засчитывается, когда мяч приземляется на оранжевом квадрате. Укажите координаты последнего квадрата, который должен быть оранжевым.

Ответ: 6F. Очки начисляются на перекрестьях, где номер соответствует месту буквы в алфавите.

20. Кремовый десерт

Какой процент крема должен заменить вопросительный знак?

Ответ: 54. Проценты состоят из всех чисел от 0 до 9, и сначала идет большее число.

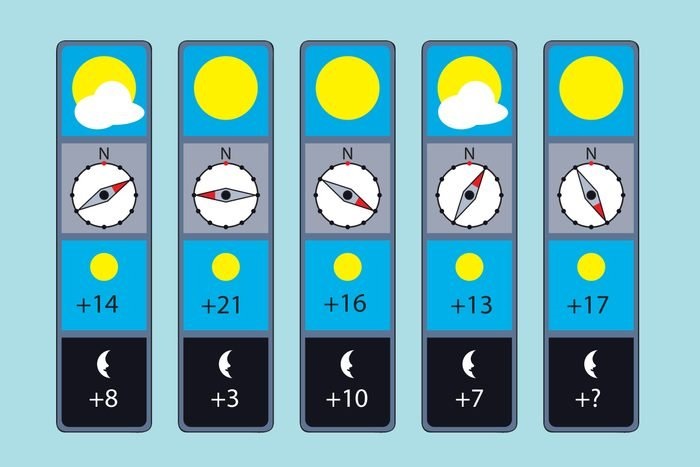
21. Холодная зона

Зная, что существует логическая связь между температурой и направлением, вычислите, какая ночная температура должна заменить вопросительный знак? (Подсказка: пришла пора жестких математических головоломок).

Ответ: 11. Замените розу ветров компаса часовым циферблатом. Красный наконечник стрелки компаса указывает на время после обеда – с 13 до 24 часов ночи – и соответствует дневной температуре. Серый наконечник указывает на утренние часы – с 1 до 12 дня – и, соответственно, определяет ночную температуру.

Математические головоломки с картинками

22. Учимся считать

Заполните каждую строку и столбец, чтобы получить конечные итоги. Используются только цифры от 1 до 9, и каждая только один раз.

Ответ:

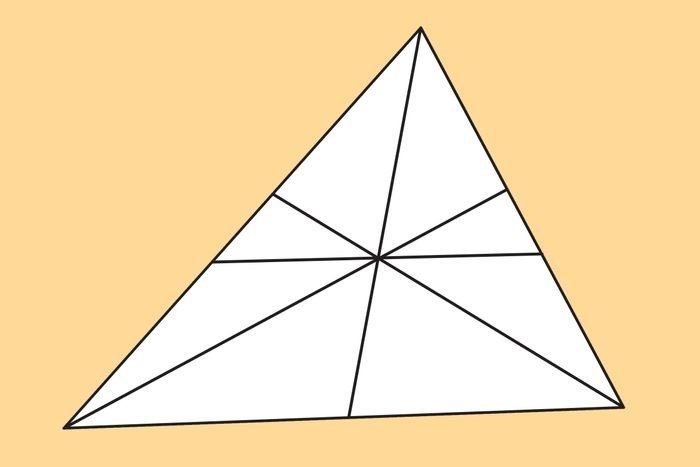
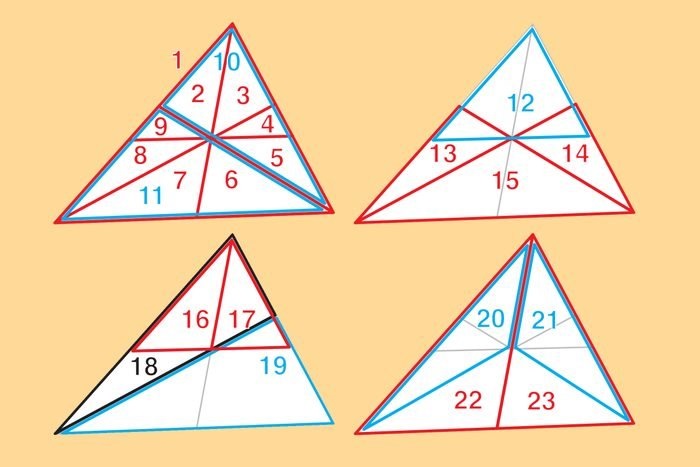
23. Хитрые треугольники

Сколько треугольников вы видите?

Ответ: 23.

24. Найди недостающее

Сколько точек должен заменить вопросительный знак на домино?

Ответ: 6 точек. Домино расположено на воображаемой сетке, а количество точек соответствует месту на этой сетке. В ней чередуются строки с числами 4 5 4 5 4 5 4 5 и 3 6 3 6 3 6 3 6.

25. Равновесие

Какой вес (AD) должен заменить вопросительный знак, чтобы весы были сбалансированы?

Ответ: B. A = B + C + D, C = B + D, A = 3D. Итак, 3D = 2B + 2D, 3D — 2D = 2B, поэтому D = 2B.

26. Ягодный секрет

Сколько недозрелых ягод не хватает на последней ветке?

Ответ: 6 ягод. В следующей ветке всегда столько же незрелых ягод, сколько спелых на предыдущей.

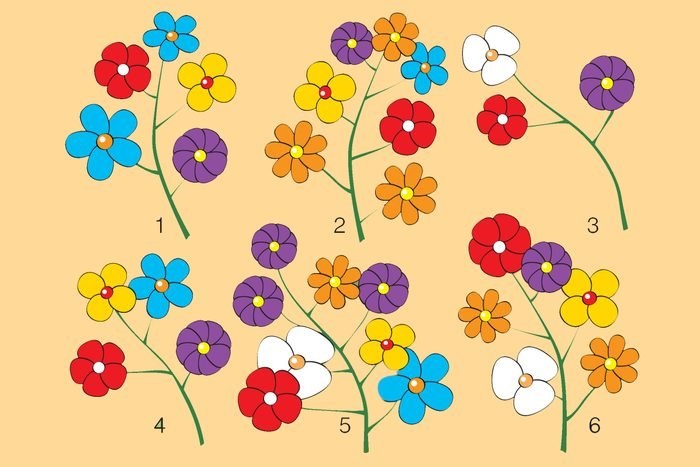
27. Цветущий сад

Какая цветочная ветвь (1-6) лишняя?

Ответ: 2. Верхний цветок всех остальных ветвей имеет столько же лепестков, сколько цветов на ветке.

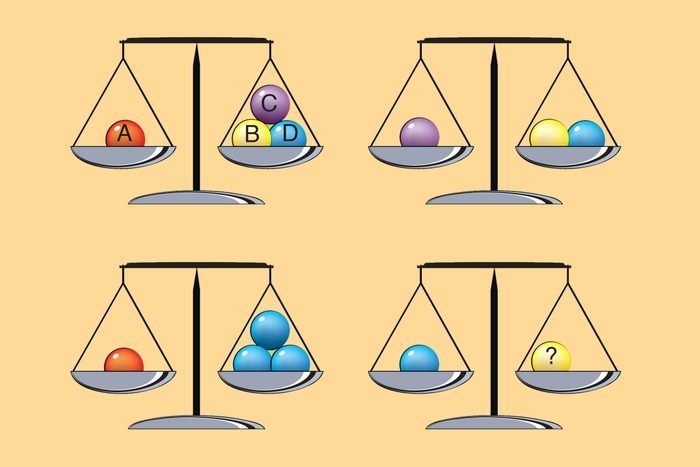
28. Игра в шарики

Какой шарик (1-6) должен заменить вопросительный знак?

Ответ: 3. Все не фиолетовые шарики сгруппированы по пять штук и образуют угол.

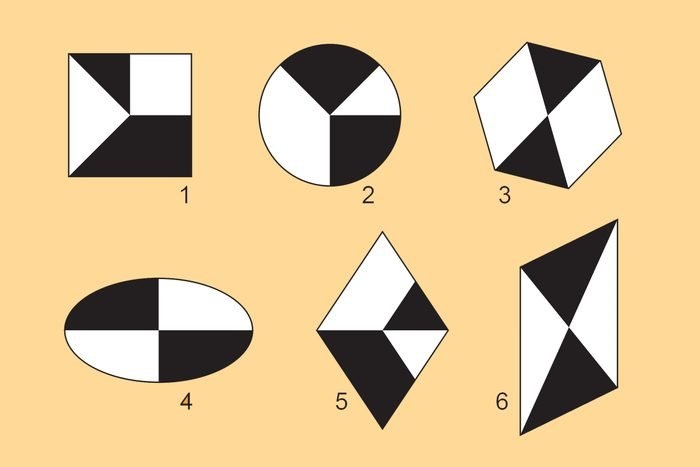
29. Форма и содержание

Какая форма (1-6) содержит больше белого, чем черного?

Ответ: 3. Все остальные содержат равные части каждого цвета.

30. Знаки-символы

В каком символе (1-6) недостает линии?

Ответ: 4. Слева направо у каждого символа есть еще одна линия.

Источник

Эффективный счёт в уме или разминка для мозга

Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:

Используем круглые числа

Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:

Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:

Упростим умножение делением

При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):

Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,

Теперь не кажется невозможным умножить в уме 625 на 53:

Возведение в квадрат двузначного числа

Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:

Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,

В общем случае (M — двузначное число):

Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:

Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.

Умножение двузначных чисел

Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:

Составив их произведение, получим:

Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:

У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:

Тогда предыдущий пример можно вычислить немного проще:

Вместо заключения

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».

Источник