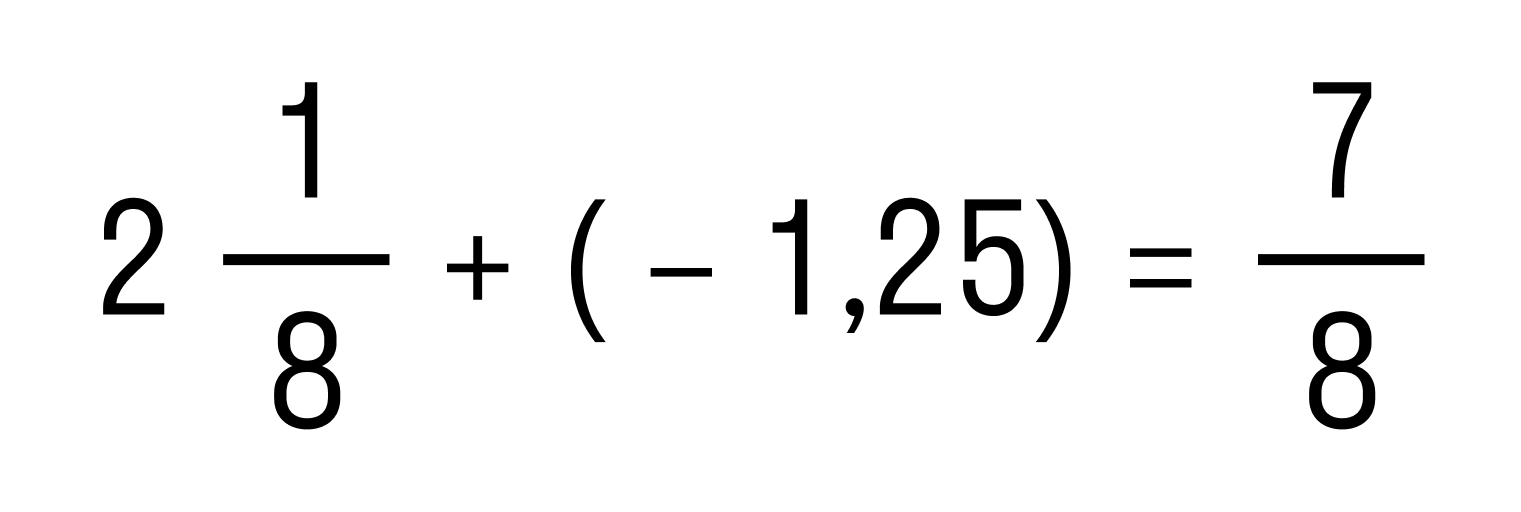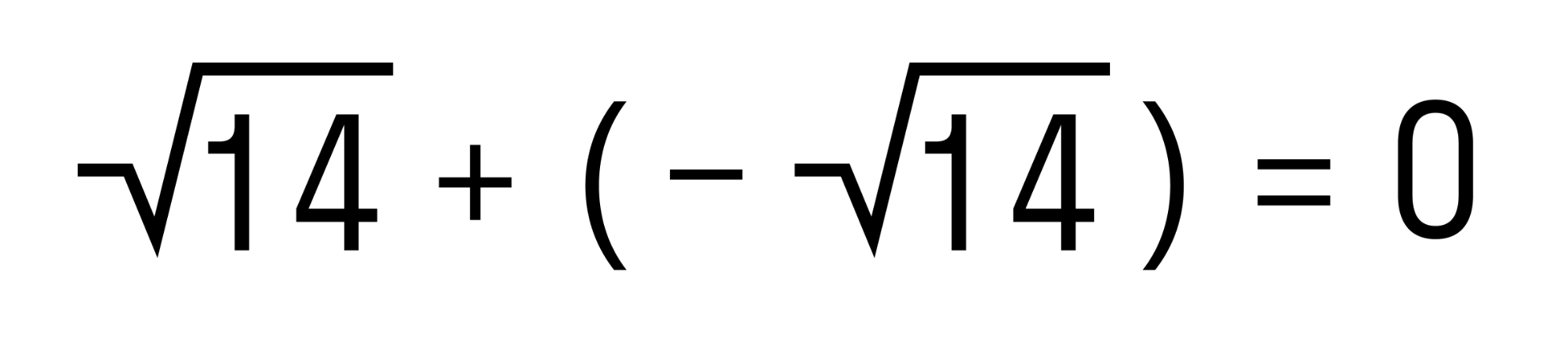- Математика
- Сложение и вычитание отрицательных чисел
- Сложение чисел с разными знаками
- Тренажер. 6 класс. Сложении и вычитание чисел с разными знаками. тренажёр по математике (6 класс)
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Сложение чисел с разными знаками
- Основные определения
- Правило сложения чисел с разными знаками
- Примеры сложения чисел с разными знаками
- Подборка задания на действия над числами с разными знаками
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Оставьте свой комментарий
- Подарочные сертификаты
Математика
План урока:
В субботу, ученики 6 класса договорились встретиться и погулять в парке. Утром Юля выглянула в окошко, ярко светит солнышко, но при этом морозно. Девочка взглянула на термометр. Он показывал -10˚C. Мама попросила Юлю пойти на улицу немного позже, когда на улице потеплеет. Юля расстроилась и стала ждать. Через два часа девочка снова взглянула на термометр. Он показал -3. Ого! Всего два часа, а так потеплело – обрадовалась девочка и стала одеваться, чтобы идти гулять. В это время в комнату вошла мама и удивленно спросила «Уже потеплело? На сколько градусов?» Дочь не знала, что сказать и как правильно узнать, на сколько градусов стало теплее. Мама пришла на помощь и сообщила, что достаточно от -10 отнять -3, и мы узнаем, на сколько градусов изменилась температура воздуха за окном. Иначе, можно сказать, что шкала термометра поднялась вверх на 7 делений, значит, на улице стало теплее на 7 градусов. Запомнив все, что рассказала мама, Юля побежала в парк делиться новыми знаниями с друзьями.
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
В театре Карабаса-Барабаса актерам жилось очень сложно, все куклы мечтали жить на свободе. Актеры тяжело работали, но долги перед хозяином росли с каждым днем. Злой владелец пообещал отпустить Буратино и Мальвину из своего театра только тогда, когда кукольные герои вернут ему долг. Сколько монет нужно собрать героям, чтобы оказаться на свободе, если у Буратино было -15 монет, а у Мальвины -6?
Чтобы ответить на главный вопрос задачи, нам нужно понимать, о чем идет речь. Изучив условие, возникает вопрос «Как может быть -15 и -6 монет?». В данном случае выходит, что Буратино и Мальвина должны вернуть Карабасу-Барабасу 15 и 6 монет, поэтому перед данными числами и стоит знак «минус». Получается, кукольные персонажи смогут покинуть театр, когда полностью вернут долг. Для этого необходимо узнать общий размер долга Буратино и Мальвины. Чтобы узнать размер долга, суммируем монеты персонажей -15 и -6. Но как их сложить, когда перед слагаемыми стоит «минус»? В подобных ситуациях применяют правило сложения отрицательных чисел.
Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.
Получается, что герои имеют -21 монету, следовательно, они должны собрать 21 монету и вернуть долг, только тогда появится возможность покинуть театр Карабаса-Барабаса.
Рассмотрим еще одно задание.
Найдите результат сложения -24 и -16.
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?
Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.
Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
- определяем модули: -3=|3|, 10=|10|;
- сравниваем модули, определяя больший: |3| 11.
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150 1 Сложить их модули, а перед результатом поставить знак «плюс»
Источник
Тренажер. 6 класс. Сложении и вычитание чисел с разными знаками.
тренажёр по математике (6 класс)
Тренажер. 6 класс. Сложении и вычитание чисел с разными знаками.
Скачать:
| Вложение | Размер |
|---|---|
| trenazher.6kl.-sraznymi_znakami.docx | 17.15 КБ |
Предварительный просмотр:
Сложение и вычитание отрицательных чисел и чисел с разными знаками.
По теме: методические разработки, презентации и конспекты
Урок-путешествие в 6 классе помогает обобщить знания, полученные при изучении темы «Сложение и вычитание положительных и отрицательных чисел».
Урок изучения нового материала. Используется презентация, тест. .
Урок «Сложение и вычитание чисел с разными знаками» 6 класс к учебнику Виленкина Н. Я. Тип урока: урок повторения и обобщения.
Данный открытый урок был разработан для передачи опыта на 5 межшкольной научной сессии » Развитие образовательной среды» в марте 2015 года. Это урок открытия новых знаний и первичного закрепления.
Обобщающий урок по теме «Сложение и вычитание чисел с разными знаками» проходит в форме игры. .
Урок содержит конспект и презентацию, по теме: «Сложение и вычитание чисел сразными знаками», а также раздаточный материал для учащихся.
Разработка урока (технологическая карта, презентация) «Сложение чисел с разными знаками» — урок формирования новых знаний и умений.Математика 6 класс: Виленкин Н. Я., Жохов В. И., Чесноков А. С., Швар.
Источник
Сложение чисел с разными знаками
О чем эта статья:
Основные определения
Целые числа — это множество чисел, которые состоят из натуральных чисел, целых отрицательных чисел и нуля.
Отрицательные целые числа — это целые числа со знаком «минус». Они всегда меньше нуля. Примеры целых отрицательных чисел: -1, -945, -20.
Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 11, 500, 1387.
У каждого положительного числа есть число-близнец, которое отличается только тем, что перед ним стоит знак минус. Такие числа называются противоположными.
Противоположные числа не равны друг другу, но у них есть общее — модуль. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного — противоположному, то есть положительному. Например:
Действительные числа — это числа, которые могут быть записаны в виде конечной или бесконечной десятичной дроби.
Рациональные числа — это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль.
Правило сложения чисел с разными знаками
Положительное число можно рассматривать как доход, а отрицательное — как расходы или долг. Чтобы понять, сколько мы заработали или потратили, нужно смотреть на модули этих чисел.
Например, родители выдали триста рублей на карманные расходы. Если в конце недели у нас осталось немного денег — значит расходов было меньше, чем дохож. А если нам пришлось попросить еще 50 рублей на наклейки — расходы привысили доход. Если же расходы равны доходам, то у нас будет нулевой остаток.
А теперь сформулируем правило сложения чисел с разными знаками.
Чтобы сложить положительное и отрицательное число, нужно:
- Найти модули слагаемых — то есть этих чисел.
- Сравнить полученные числа.
Если они равны, то исходные слагаемые противоположны друг другу (те самые близнецы) — их сумма равна нулю. А если же числа не равны, то нужно запомнить знак числа, модуль которого больше. - Из большего модуля вычесть меньший.
- Перед полученным числом поставить знак того слагаемого, модуль которого больше.
Это правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшее число. В результате сложения положительного и отрицательного числа может получиться: положительное число, отрицательное число или нуль.
Вот, как выглядит эта последовательность на примере 2 + (-6) = -4:
| Знаки слагаемых | Знак суммы | Модули слагаемых | Модуль суммы | Разность модулей слагаемых | Сравнение знака суммы со знаками слагаемых |
| Разные | «−» | ∣2∣ = 2 ∣-6∣ = 6 | ∣-4∣ = 4 | ∣-6∣ — ∣2∣ = 4 6 — 2 = 4 | Знак результата (-4) такой же, как и у числа, которое больше по модулю (-6) |
Повторим еще раз. Чтобы сложить числа с разными знаками:
- из большего модуля вычесть меньший модуль;
- в результате поставить знак слагаемого с большим модулем.
Алгоритм сложения чисел с разными знаками справедлива для целых чисел, для рациональных чисел и для действительных чисел.
Примеры сложения чисел с разными знаками
Сложение чисел с разными знаками требует внимательности и последовательности. Рассмотрим примеры по правилу выше:
Пример 1. Сложить числа -8 и 1.
Нам нужно сложить числа с разными знаками. Выполним все шаги по правилу сложения положительного и отрицательного числа.
- Сначала найдем модули слагаемых, они равны 8 и 1 соответственно.
- Модуль числа -8 больше, чем модуль числа 1. Запомним знак минус.
Теперь от большего модуля отнимаем меньший модуль:
8 — 1 = 7. - Осталось поставить знак минус перед полученным числом, получаем ответ: -7.
На этом сложение чисел с разными знаками завершено.
Пример 2. Сложить положительное число 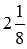
Чтобы сложить рациональные числа с разными знаками, которые не являются целыми, их следует представить в виде обыкновенных или десятичных дробей.
- Представим числа в виде обыкновенных дробей.
Для этого выполним переход от смешанного числа к неправильной дроби:, и переводим десятичную дробь в обыкновенную:
- Теперь можно воспользоваться правилом сложения чисел с разными знаками.
Модули складываемых чисел равны 17/8 и 5/4. Чтобы нам было удобнее считать, приведем дроби к общему знаменателю — получаем 17/8 и 10/8. - Сравним обыкновенные дробей 17/8 и 10/8.
Так как 17>10, то. Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс.
- Теперь из большего модуля вычитаем меньший, то есть, выполним вычитание дробей с одинаковыми знаменателями:
Осталось перед полученным числом поставить знак плюс, получаем:, то есть 7/8.
На этом сложение чисел с разными знаками завершено. Краткая запись решения выглядит так:
Пример 3. Чему равна сумма чисел 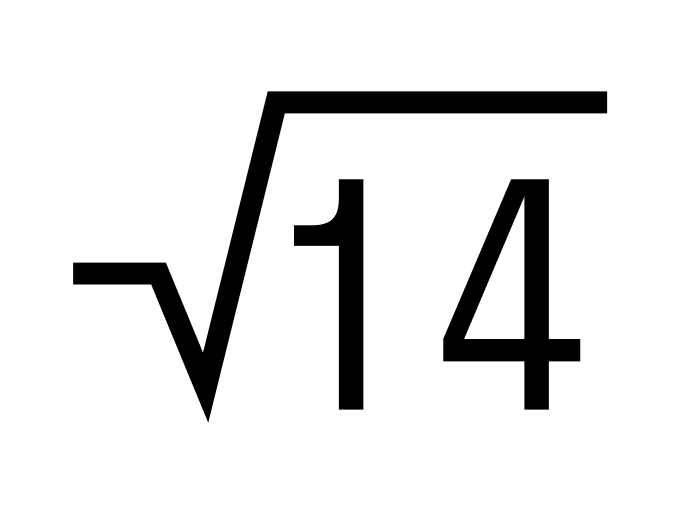
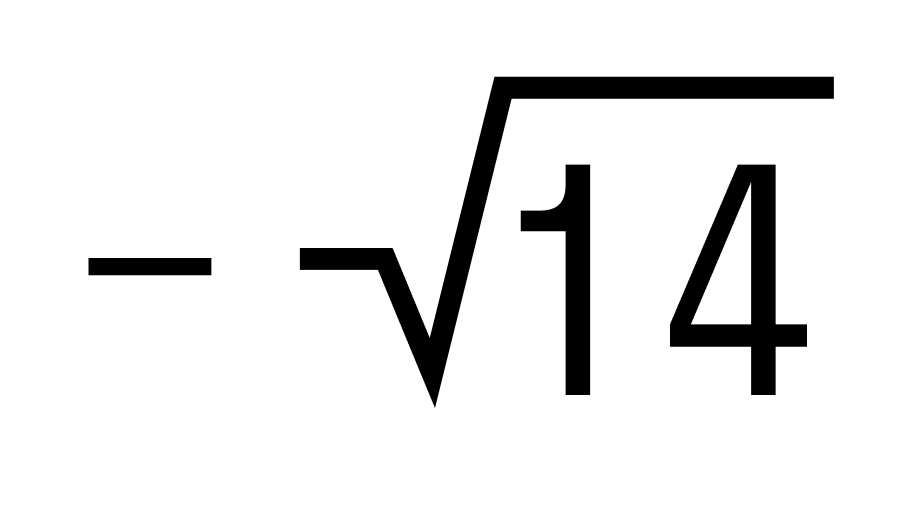
Замечаем, что у складываемых чисел разные знаки, а их модули равны. Значит эти числа являются противоположными, а сумма противоположных чисел равна нулю.
Получается вот так:
Важно помнить, что при сложении действительных чисел с разными знаками результат можно записывать не в виде бесконечной десятичной дроби, а в виде числового выражения, которое содержит корни, степени, логарифмы и прочее.
- Например, результат сложения двух чисел с разными знаками -1 и π записывается так: π — 1.
Источник
Подборка задания на действия над числами с разными знаками
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Онлайн-конференция для учителей, репетиторов и родителей
Формирование математических способностей у детей с разными образовательными потребностями с помощью ментальной арифметики и других современных методик
Международная дистанционная олимпиада Осень 2021
Номер материала: ДБ-122670
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Путин назвал уровень доходов преподавателей одним из социальных приоритетов
Время чтения: 1 минута
В России будут разработаны меры по усовершенствованию системы оплаты труда педагогов
Время чтения: 1 минута
Путин поручил сократить количество контрольных работ в школах
Время чтения: 1 минута
Студенческие кампусы появятся в восьми регионах России до конца 2025 года
Время чтения: 2 минуты
Больше половины самых конкурентоспособных школ в России находятся в регионах
Время чтения: 4 минуты
В пяти регионах России протестируют новую систему оплаты труда педагогов
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник

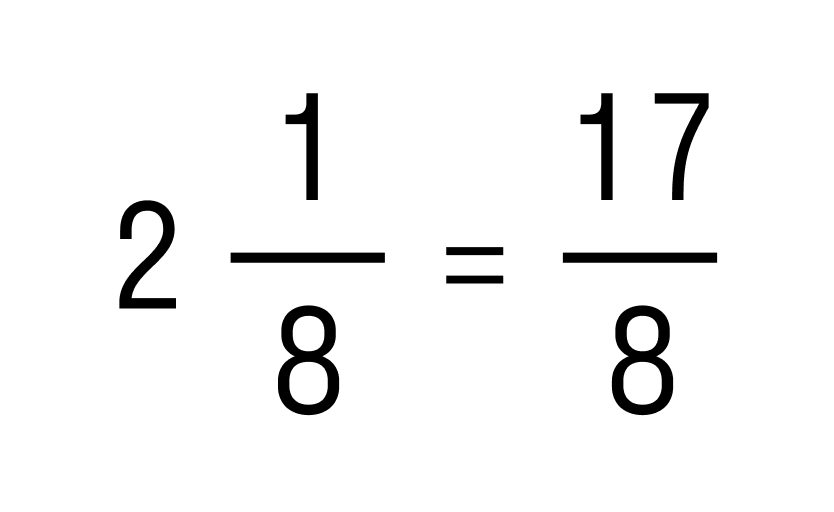 , и переводим десятичную дробь в обыкновенную:
, и переводим десятичную дробь в обыкновенную: 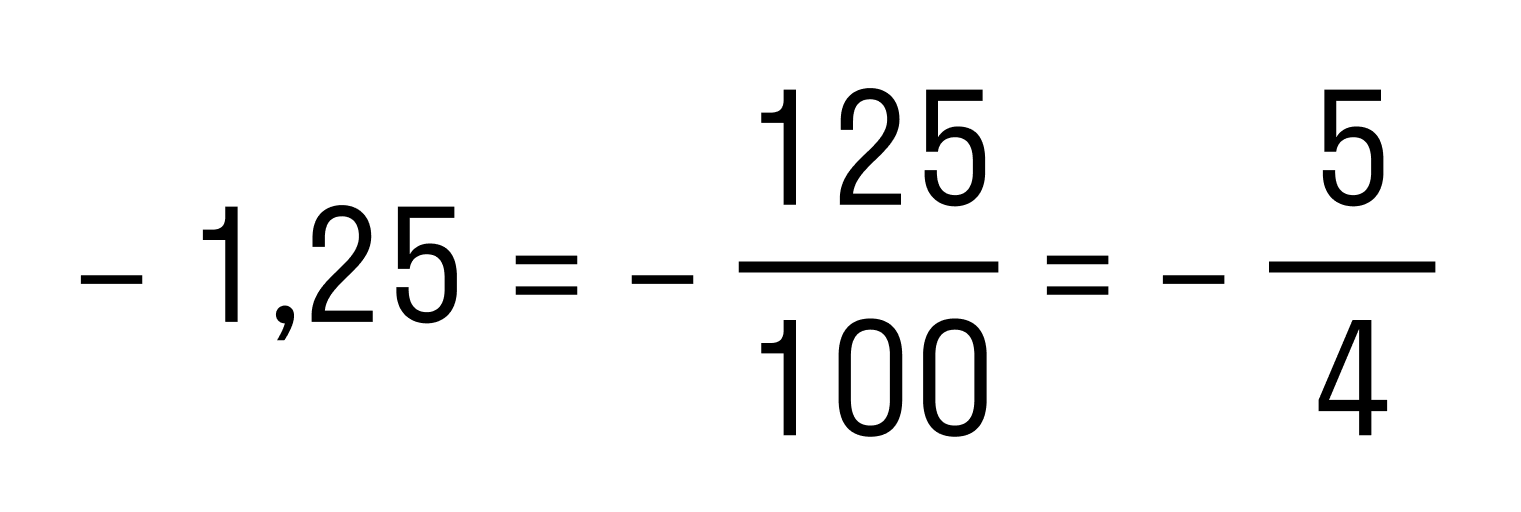
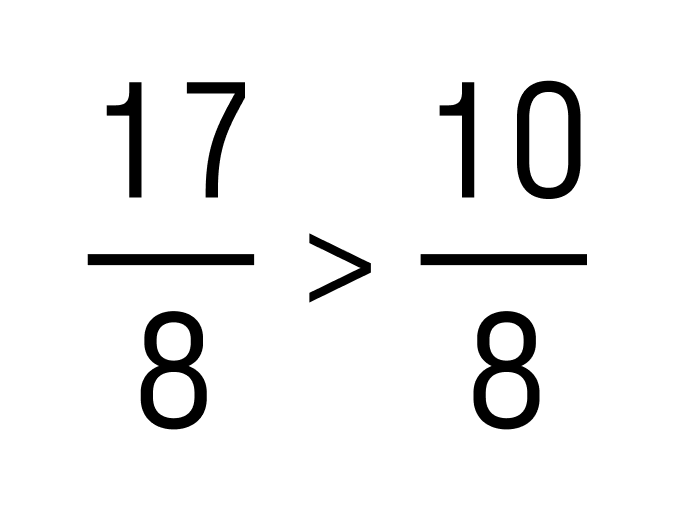 . Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс.
. Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс. 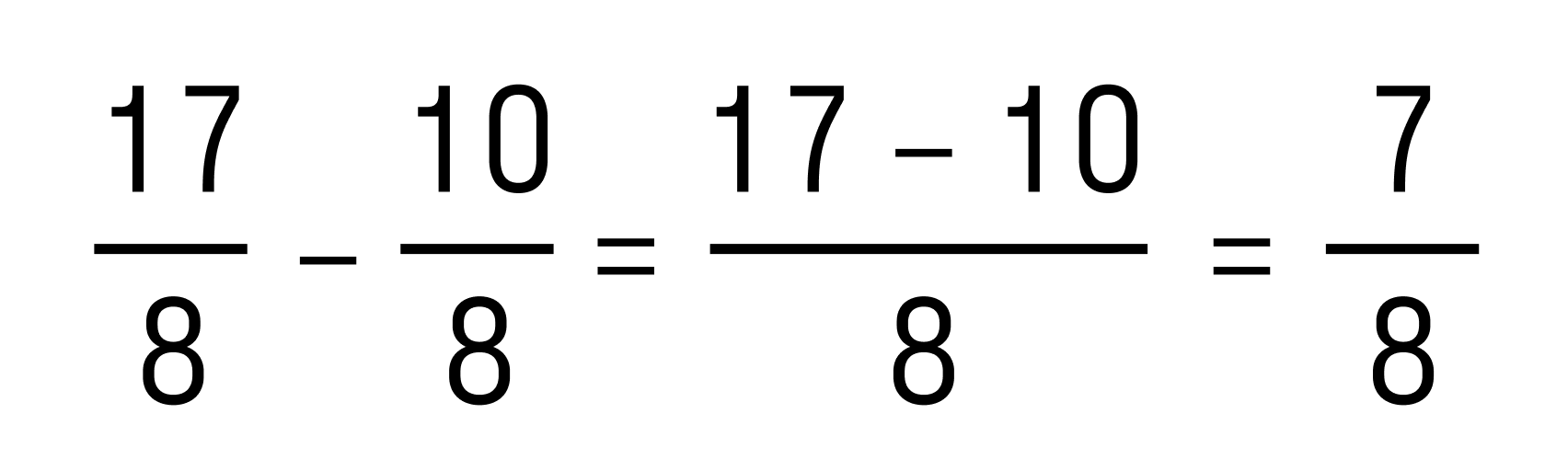
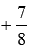 , то есть 7/8.
, то есть 7/8.